Principle Component Analysis (PCA)
Apart from clustering, dimension reduction is another type of unsupervised machine learning method. This method is widely applied in the following:
-
Data Compression - where we reduce our dimension of our features if we have a lot of redundant data, i.e. we find two highly correlated feature, plot them, then make a new line that seems to describe both features accurately. By performing data compression, we reduce the total data we have to store in our computer and will eventually speed up our learning algorithm.
-
Visualization - to reduce the dimension of our data to 3 or less in order to plot it, since it is nearly impossible to visualie datat that is more than three dimensions.
Principle Component Analysis (PCA)
PCA is the one of the most popular dimensionality reduction algorithm and the goal is to reduce the average of all the distances of every feature to the projection line, i.e. the projection error. The general case is as follows:
We aim to reduce the dataset from dimension to dimension, where we find vectors onto which project the data so as to minimize the projection error (orthogonal project from the point to the plane). For instance, if we are trying to reduce 3D to 2D, we will project the data onto two directions, therefore our will be 2.
PCA may sound very similar to Linear Regression, however, they are not. In Linear Regression, what we are trying to achieve is to minimize the squared error from every point to our predictor line and they are the vertical distances in which we are taking all our examples in and applying some parameters in to predict . Linear Regression is supervised learning.
On the contrary, in PCA, what we are trying to achieve is to minimize the shortest orthogonal distances (90-degree) to our data points in which we are taking a number of features and find the closest common dataset among them. No predictions are involved. PCA is unsupervised learning.
Figure 1 illustrates the difference between this two machine learning algorithm.
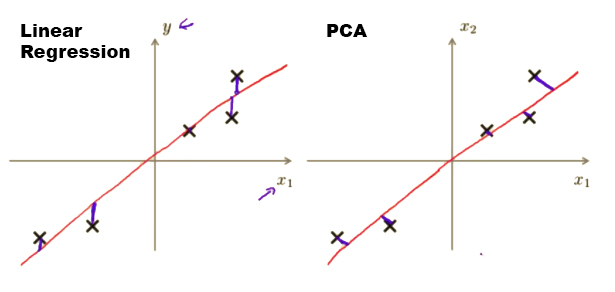Figure 1: Linear Regression is not PCA.
PCA Algorithm
Before applying PCA, it is important to first pre-process your data using feature scaling or mean normalization. The PCA algorithm is formulated using these steps:
- Compute ‘Covariance Matrix’ -
- Compute ‘Eigenvectors’ of Covariance Matrix
- Take the first columns of the principle components and compute .
To have a better understanding of covariance, eigenvectors and how they relate to PCA, try checking out these very informative links:
- Why is the eigenvector of a covariance matrix equal to a principal component?
- What is the importance of eigenvalues/eigenvectors?
- Why do eigenvalues matter? What are their real world applications?
To summarize, the whole algorithm implemented in Matlab/Octave is as below:
% compute the covariance matrix
Sigma = (1/m) * X' * X;
% compute our projected directions
[U,S,V] = svd(Sigma);
% take the first k directions
Ureduce = U(:,1:k);
% compute the projected data points
Z = X * Ureduce;
To better understand PCA in general, we will first perform some simple experiment on an example 2D data. As usual, let us first visualize the scatter plot of our 2D sample data.
Figure 2: Sample 2D data.
After running Step 1 and Step 2 to compute the principle components , we can plot the corresponding principle components like in Figure 3.
Figure 2: Plotting the principle components of the dataset.
It is also interesting to note that we can reverse this process, i.e. reconstructing an approximate of the data. After projecting the data onto lower dimension(s), we can approximately recover the data by projecting them back onto the original dimensional space. We can do this by using this equation . Figure 3 illustrate the idea of reconstructing the approximate of the data.
Figure 3: The original and projected data after PCA
In Figure 3, the original data points are indicated with blue circles, while the projected data points are indicated with red circles.
PCA on Face Images
Now let us try PCA on Face Images dataset, where each face image is 32 x 32 in grayscale (1024 dimensions). Let us have a look at these pretty faces before running PCA on them.
Figure 4: Face dataset
To understand how the number of principle components, , affects the compression process, we will gradually increase the number of and understand how they affect compression output. We tried using = 4,12,36, and 100. The compression results are showed in Figure 5 to Figure 8 respectively. Essentially, the goal is PCA is to reduce dimensionality in order to speed up our learning algorithm.
Figure 5: PCA with 4 principle components
Figure 6: PCA with 12 principle components
Figure 7: PCA with 36 principle components
Figure 8: PCA with 100 principle components
Given our original dataset of 1024 dimensions, notice how PCA is able to reduce it down to 100 dimensions without significant lost of the features on each of the faces. Pretty remarkable!
Finally, we can reconstruct our compressed face images using the top 100 principal components as shown in Figure 9. Notice after the reconstruction, we can observe that the general feature and appearance of the face are kept while the fine details are lost.
Figure 9: Original faces on the left vs. Recovered faces on the right
Choosing the Number of
Remember the previous Matlab/Octave implementation where
[U,S,V] = svd(Sigma)
We can use S which is a diagonal matrix and help us determine the appropriate number of . We can check for 99% of retained variance using the S matrix as follows
However, as Ng suggests, any number greater than 0.85 (85%) is still an acceptable percentage to report that your PCA algorithm is still working fine!
To wrap it up, the goal of PCA is to reduce dimensionality of data, speed up learning algorithm and data visualization. It is also important to note that we try not to assume we need to do PCA. We should try our learning without PCA and also use PCA if necessary.